レヴィ=ストロースの「構造」について
読書メモ:レヴィ=ストロース入門より(2)
引き続き「レヴィ=ストロース入門」(著:小田亮 ちくま新書)からのメモになります。
今回は主に第二章の「構造主義はどのように誤解されるか」から、
レヴィ=ストロースの<構造>について、理解を深めたいと思います。
この本には構造主義といういわゆる<構造>という言葉が
誤解を生みやすい言葉である、と指摘されています。
構造主義を理解するには、当然のことながら、その<構造>という概念を把握する必要があるが、にもかかわらず、これほど誤解されている概念もめずらしい・・・構造というと、ビルなどの建造物の構造とか、会社などの社会組織の構造などのように、動かない固定されたもので、その全体を支配しているものとイメージされることが多いのではないか。(P44)
wikiやコトバンクには、以下のような説明が書かれてあります。
構造(こうぞう、英:structure)とは、ひとつのものを作りあげている部分部分の組み合わせかた。ひとつの全体を構成する諸要素同士の、対立・矛盾・依存などの関係の総称。複雑なものごとの 部分部分や要素要素の 配置や関係。(wiki)
1 一つのものを作り上げている部分部分の材料の組み合わせ方。また、そのようにして組み合わせてできたもの。仕組み。「家の構造」「体の構造」「文章の構造」「構造上の欠陥」
2 物事を成り立たせている各要素の機能的な関連。また、そのようにして成り立っているものの全体。「汚職の構造が明らかになる」「経済の二重構造」「社会構造」「精神構造」(デジタル大辞泉の解説―コトバンク)① 全体を形づくっている種々の材料による各部分の組み合わせ。作りや仕組み。 「機械の-」 「耐震-」② さまざまな要素が相互に関連し合って作り上げている総体。また、各要素の相互関係。 「社会-」 「精神-」 「物質の-」 「文の-」 「汚職の-」(大辞林 第三版の解説―コトバンク)
つまり、<構造>とは「仕組み」とほぼ同じであるようです。
仕組みはそれが動いている間は基本固定しているので、
「固定したイメージ」というものがわかります。
そしてそれは「システム(体系)」と言い換えられる言葉といえます。
「ある社会の親族の構造」とか「ある神話の構造」といった用法も、構造主義の<構造>という概念からはずれている。これらの用法では、構造という語は、体系とほとんど同じ意味に使われているが、レヴィ=ストロースの<構造>概念は、体系とはっきり区別されているものである。(P45)
そうした混乱を避け、違いを明確にすることが、
レヴィ=ストロースの構造主義を理解するためには必要ということのようです。
そしてその鍵となるのが、「変換」という概念と、「不変」の概念との関係。
レヴィ=ストロースの構造主義における<構造>概念を理解する鍵は、<構造>と呼ばれるものと体系と呼ばれるものの違いを理解することにある。そして、その違いのポイントは、<構造>が変換transformationという概念と一体であるということにあり、さらに、その変換と不変の概念との結びつきにある。(P47)
要素も要素のあいだの関係もすべて変化しているにもかかわらず、そこに現れる「不変の関係」という不思議なものが<構造>ということになる。(P48)
構造における「変換を通じて不変なもの」とは要素間の関係のことだと誤解する(P51)
<構造>という見方の本領は、体系を支配する「一つの内的脈絡」が「一つの切り離された体系の観察に置いては近づきえないものでありながら、変換の研究― それによって、一見異なった体系の間に類似性をみいだすことができる― において明らかになる」(「人類学の課題」)ようなときにこそ発揮される。・・・それがみつかる場は、いわば、体系と体系との<あいだ>なのである。(P51)
もう分からなくなってきました(笑)。
でも少なくとも、
一つの対象だけを見ていても、その中にはレヴィ=ストロースの<構造>は見つからない。
複数の対象を必要とすることのようです。
さて、ここで図をご紹介します。
レヴィ=ストロースが「変換」という概念で影響をうけたものとして出てくるものです。
アルブレヒト・デューラーの「人体比例論」

そしてダーシー・トムソンの「生物のかたち」に掲載れている魚の図です。
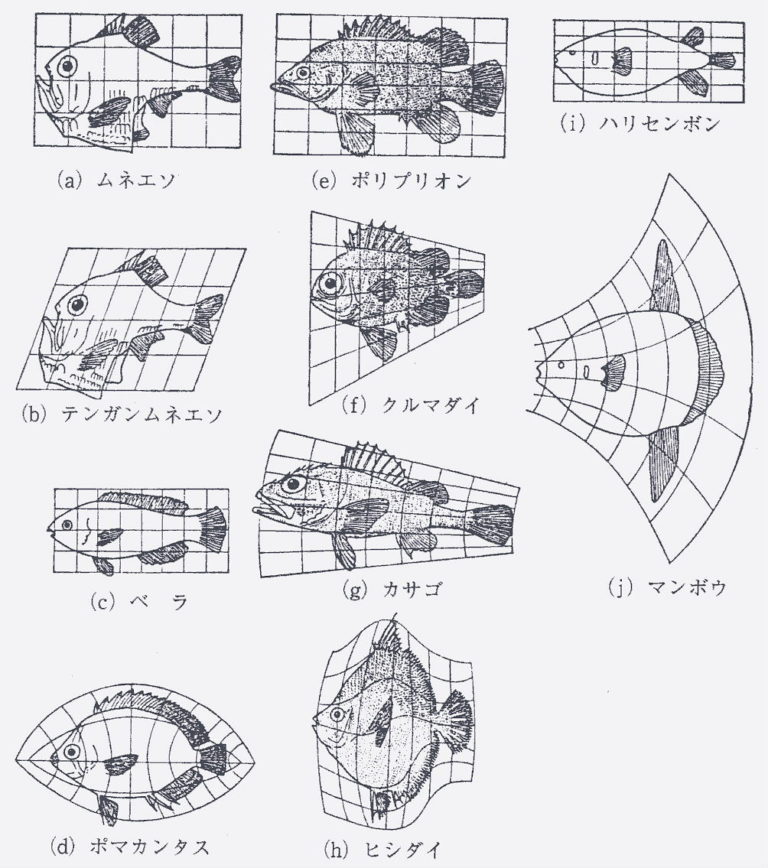
デューラーの図は異なる横顔を、
ダーシー・トムソンの図は異なる魚をそれぞれ座標で区切って、
要素の配列の位置関係がいろいろと変わっているような図と言えそうです。
「変換」という概念を示す例としてのこの図は、
例えば、(i)のハリセンボンと、(j)のマンボウ
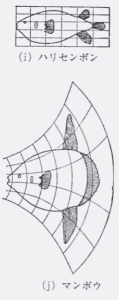
これらは、図柄が同じですが、
各要素の大きさが異なること(位相変換)で別の魚です。
つまりこの図で言えば、位相変換(伸び縮み)されているそれぞれの関係、
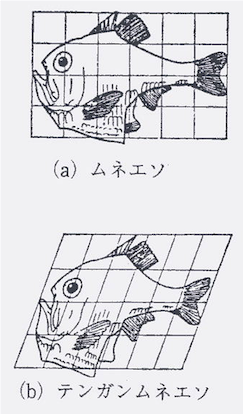
(a)ムネエソ と (b)テンガンムネエソ (この場合は射影変換というらしい)
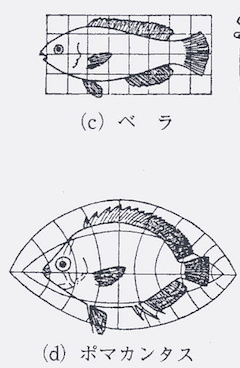
(c)ベラ と (d)ポマカンタス
(e)ポリプリオン と (f)クルマダイ と (g)カサゴ と(i)ヒシダイ
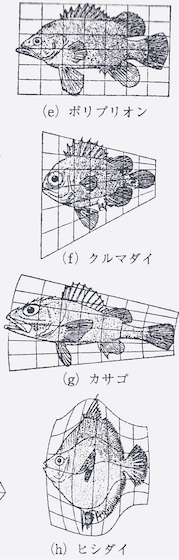
(i)ハリセンボン と (j)マンボウ
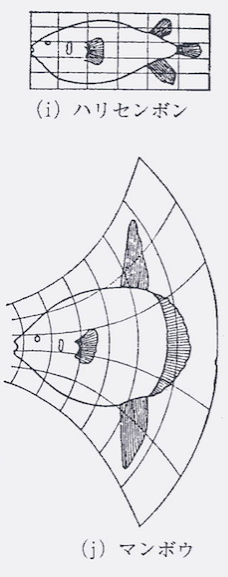
これらには位相的性質をもつ<構造>がみられる、ということとも言えるようです。
都合よくいくらでも伸びたり縮んだりするゴム膜の上に、図形を書いて、伸び縮みさせながら別の図形に重ねることができるかを、考えてみる。この変換が、位相変換である。位相変換に関して不変な性質を位相的性質という。これもまた、<構造>である。(『はじめての構造主義』)(P57)
(h)のヒシダイは(e)ポリプリオンと同じ要素ではないように見えますが、
「さらに特異な変形によって(トムソン『生物のかたち』)(P53)」
とあるように、厳密に全く同じ要素である必要もなさそうです。
ですがこのそれぞれの要素が異なる
(a)ムネエソと(e)ポリプリオンと(i)ハリセンボン
これらには伸び縮みした位相変換ではありませんし、
(a)ムネエソ と (b)テンガンムネエソのように、斜めにしただけの射影変換でもありません。
それでもこれらもまた同じ<構造>と言えるのでしょうか?
ですが、おそらくこの質問は間違っているような気がしてきました。
このトムソンの図そのものが、レヴィ=ストロースの<構造>を示す例ではなく、
あくまで、伸びたり縮んだりする変換で違う魚になったり、
それでも変わらない性質が見いだせる例の一つとしてあるだけだからです。
(必要なのは(i)ハリセンボンと(j)マンボウとの変換のようなパターンについてだけなんだと考え直しました)
これらの位相変換などといった変換の概念は、「数学的」な概念として
レヴィ=ストロースの<構造>概念の理解のために大切な要素とあります。
<構造>と<変換>との表裏一体の関係、いいかえれば<変換>と<構造>の不変性との関係こそ、その<構造>概念を理解するうえでの最も重要な鍵であり、それを理解していないことが、これまでの誤解のほとんどの原因であったからである。(P64)
そしてレヴィ=ストロースの<構造>の概念には
この数学的な概念のものとともに、
ソシュールの言語学からの影響など複数の要素が重なり合ってできたものということです。
レヴィ=ストロースの構造概念は、この形態学的・数学的な変換の概念のほかにも、ヤーコブソンの構造言語学や文化人類学など、それとは異なる源泉から取りだされた諸観念が重なり合ってできたものであった。(P65)
ということで、次があるとすれば、
ソシュールやヤーコブソンの言語学からの<構造>についてでしょうか・・・
